


/中文/

/中文/

/中文/

/中文/

/中文/

/中文/

/中文/

/中文/

/中文/

/中文/
对于计算器小编有自己独到的想法!在卡方检验计算器最新版中您可通过这款计算器软件快速计算出测量的数据是否准确,并且在卡方检验计算器最新版中如果实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0哦!

方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。
注意:卡方检验针对分类变量。
(1)提出原假设:
H0:总体X的分布函数为F(x).
如果总体分布为离散型,则假设具体为
H0:总体X的分布律为P{X=xi}=pi, i=1,2,...
(2)将总体X的取值范围分成k个互不相交的小区间A1,A2,A3,…,Ak,如可取A1=(a0,a1],A2=(a1,a2],...,Ak=(ak-1,ak),
其中a0可取-∞,ak可取+∞,区间的划分视具体情况而定,但要使每个小区间所含的样本值个数不小于5,而区间个数k不要太大也不要太小。
(3)把落入第i个小区间的Ai的样本值的个数记作fi,成为组频数(真实值),所有组频数之和f1+f2+...+fk等于样本容量n。
(4)当H0为真时,根据所假设的总体理论分布,可算出总体X的值落入第i 个小区间Ai的概率pi,于是,npi就是落入第i个小区间Ai的样本值的理论频数(理论值)。
(5)当H0为真时,n次试验中样本值落入第i个小区间Ai的频率fi/n与概率pi应很接近,当H0不真时,则fi/n与pi相差很大。基于这种思想,皮尔逊引进如下检验统计量 ,在0假设成立的情况下服从自由度为k-1的卡方分布。
当两个样本资料中有发生数和未发生数时可使用此方法计算X2值及P值范围,在输入四个数字后回车或点击计算按钮可在右上结果栏中显示计算结果,其它计算方法相似。
当两个样本资料中分别有样本数和发生数时可使用此方法计算X2值及P值范围。
当两个样本资料中分别有样本数和发生率时可使用此方法计算X2值及P值范围。

 数字排列组合生成器(计算排列组合)计算器类
/ 9K
数字排列组合生成器(计算排列组合)计算器类
/ 9K
 Windows计算器win10版(系统计算器) 绿色版计算器类
/ 737K
Windows计算器win10版(系统计算器) 绿色版计算器类
/ 737K
 AxMath特别版(数学公式编辑器) v2.6.1 最新版计算器类
/ 10M
AxMath特别版(数学公式编辑器) v2.6.1 最新版计算器类
/ 10M
 RBCCE官方版(路桥施工计算专家) 2017 免费版计算器类
/ 79M
RBCCE官方版(路桥施工计算专家) 2017 免费版计算器类
/ 79M
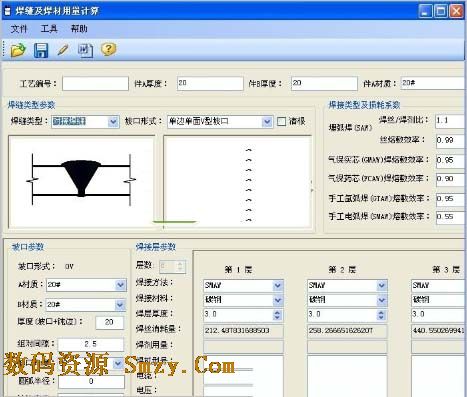 焊缝及焊材用量计算器v2.0.0.8 绿色免费版计算器类
/ 449K
焊缝及焊材用量计算器v2.0.0.8 绿色免费版计算器类
/ 449K
 计算不规则多边形面积软件绿色版(计算工具) v2.0.4 官方版计算器类
/ 5M
计算不规则多边形面积软件绿色版(计算工具) v2.0.4 官方版计算器类
/ 5M
 CRC16校验码计算器(计算CRC16校验码工具) v1.2 免费版计算器类
/ 376K
CRC16校验码计算器(计算CRC16校验码工具) v1.2 免费版计算器类
/ 376K
 AC钢构官方版(钢材料预算软件) v6.1 免费版计算器类
/ 11M
AC钢构官方版(钢材料预算软件) v6.1 免费版计算器类
/ 11M
 司法速算器免费版(司法工作计算工具) v16 绿色版计算器类
/ 451K
司法速算器免费版(司法工作计算工具) v16 绿色版计算器类
/ 451K
 现代鲁班工程量计算书v3.5.009 绿色免费版计算器类
/ 2.15M
现代鲁班工程量计算书v3.5.009 绿色免费版计算器类
/ 2.15M
 数字排列组合生成器(计算排列组合)计算器类
/ 9K
数字排列组合生成器(计算排列组合)计算器类
/ 9K
 Windows计算器win10版(系统计算器) 绿色版计算器类
/ 737K
Windows计算器win10版(系统计算器) 绿色版计算器类
/ 737K
 AxMath特别版(数学公式编辑器) v2.6.1 最新版计算器类
/ 10M
AxMath特别版(数学公式编辑器) v2.6.1 最新版计算器类
/ 10M
 RBCCE官方版(路桥施工计算专家) 2017 免费版计算器类
/ 79M
RBCCE官方版(路桥施工计算专家) 2017 免费版计算器类
/ 79M
 焊缝及焊材用量计算器v2.0.0.8 绿色免费版计算器类
/ 449K
焊缝及焊材用量计算器v2.0.0.8 绿色免费版计算器类
/ 449K
 计算不规则多边形面积软件绿色版(计算工具) v2.0.4 官方版计算器类
/ 5M
计算不规则多边形面积软件绿色版(计算工具) v2.0.4 官方版计算器类
/ 5M
 CRC16校验码计算器(计算CRC16校验码工具) v1.2 免费版计算器类
/ 376K
CRC16校验码计算器(计算CRC16校验码工具) v1.2 免费版计算器类
/ 376K
 AC钢构官方版(钢材料预算软件) v6.1 免费版计算器类
/ 11M
AC钢构官方版(钢材料预算软件) v6.1 免费版计算器类
/ 11M
 司法速算器免费版(司法工作计算工具) v16 绿色版计算器类
/ 451K
司法速算器免费版(司法工作计算工具) v16 绿色版计算器类
/ 451K
 现代鲁班工程量计算书v3.5.009 绿色免费版计算器类
/ 2.15M
现代鲁班工程量计算书v3.5.009 绿色免费版计算器类
/ 2.15M