

249的因数探索之旅
在数学的世界里,每一个数字都蕴藏着独特的奥秘,等待着我们去发掘。今天,我们将踏上一场关于数字249的因数探索之旅,一同揭开它背后的神秘面纱。
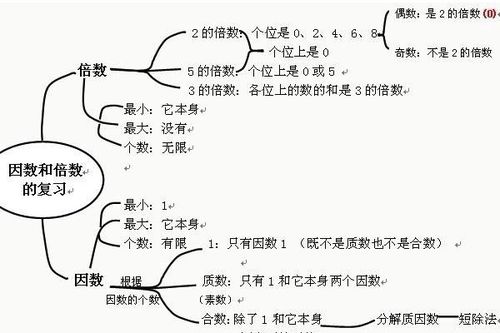
首先,我们需要明确什么是因数。因数,又称约数,是指能够整除给定整数的正整数。例如,对于数字6,它的因数有1、2、3和6,因为这些数都能整除6而不留余数。同样地,对于数字249,我们也需要找出所有能整除它的正整数。
为了找到249的因数,我们可以采用试除法。试除法是一种简单而有效的寻找因数的方法,它基于以下原理:如果一个数a能被另一个数b整除,那么a除以b的商c也必定是一个整数。因此,我们可以从1开始,逐一尝试每一个小于或等于249的正整数,看它们是否能整除249。
当然,在实际操作中,我们并不需要真的去尝试每一个数。因为一旦我们找到了一个因数,就可以利用这个因数来找到另一个因数(即249除以这个因数的结果)。此外,我们还可以利用一些数学技巧来缩小搜索范围,比如只考虑249的质因数分解形式中的质因数及其组合。
不过,为了保持文章的通俗性和易读性,我们还是采用最直观的试除法来展示这个过程。
首先,我们尝试用1去除249,结果是249,说明1是249的一个因数。接着,我们尝试用2去除249,发现不能整除,所以2不是249的因数。然后,我们尝试用3去除249,结果是83,说明3和83都是249的因数。
继续这个过程,我们发现5、7等较小的数都不能整除249。当我们尝试用更大的数去除时,我们发现了一些有趣的规律。比如,当我们用13去除249时,虽然不能直接整除,但我们可以发现249与13的乘积非常接近但略大于一个已知的因数(比如39,因为39是13的3倍,而3是249的一个因数)。这提示我们,可以尝试将249分解为两个数的乘积,其中一个数是我们已知的因数,另一个数则是我们尚未发现的因数。
然而,在这个特定的例子中,我们并不需要真的去尝试所有可能的组合。因为我们已经找到了一个因数3,并且知道249除以3的结果是83。这意味着,除了1和249本身之外,249的因数只有3和83这两个。
为了验证我们的结果,我们可以使用另一种方法:质因数分解。质因数分解是将一个正整数表示为若干个质数的乘积的过程。对于249来说,我们可以尝试找到它的所有质因数,并将它们组合起来以得到原始的数。
通过观察249的各位数字和尝试一些常见的质数作为除数,我们发现249可以被3整除。因此,3是249的一个质因数。接下来,我们将249除以3得到83,并发现83是一个质数(因为它只能被1和自己整除)。所以,249的质因数分解形式是3乘以83。
这个结果与我们之前通过试除法找到的结果是一致的:249的因数有1、3、83和249。其中,1和249是任何正整数的因数(即平凡因数),而3和83则是249的非平凡因数(即除了1和本身以外的因数)。
在探索249的因数的过程中,我们不仅学会了如何找到一个数的因数,还了解了质因数分解的概念和方法。这些知识和技能在数学、物理、计算机科学等领域都有着广泛的应用。比如,在密码学中,质因数分解是许多加密算法的基础;在优化问题中,找到问题的最小因数或最大因数往往能帮助我们更快地找到解决方案。
此外,探索数字的因数还能激发我们对数学的兴趣和好奇心。当我们发现一个新的因数时,那种成就感和满足感是无法用言语来表达的。而这种好奇心和成就感正是推动我们不断学习和探索数学世界的强大动力。
回到249的因数这个话题上,我们还可以进一步思考一些问题。比如,249有多少个因数?这些因数之间有什么关系?它们能否构成一个有趣的数列或图形?这些问题虽然看似简单,但背后却隐藏着深刻的数学原理和规律。通过深入思考和探索这些问题,我们可以更好地理解数学的本质和魅力所在。
总之,探索249的因数不仅是一次有趣的数学冒险之旅,更是一次对数学知识和技能的全面锻炼和提升。在这个过程中,我们不仅学会了如何找到一个数的因数、如何进行质因数分解等基本技能和方法;还培养了我们的观察力、思考力和解决问题的能力;更重要的是,我们激发了对数学的兴趣和好奇心,为未来的学习和探索奠定了坚实的基础。希望每一位读者都能在这场探索之旅中收获满满的知识和快乐!